Le théorème de Pythagore est une équation mathématique qui permet de calculer l’hypoténuse d’un triangle rectangle. Elle est utilisée depuis l’Antiquité et est considérée comme l’une des équations les plus importantes et fondamentales des mathématiques. Donc, comment à quoi sert le théorème de Pythagore ?
Théorème de Pythagore : cours
Définition du théorème de Pythagore ?
Le théorème de Pythagore est une propriété mathématique qui s’applique aux triangles rectangles.
Selon cette théorie, la somme des carrés des deux côtés adjacents à l’angle droit est égale au carré de l’hypoténuse, qui est le côté opposé à l’angle droit.
En d’autres termes, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des deux autres côtés du triangle. Cette formule est souvent utilisée pour calculer la longueur d’un côté d’un triangle rectangle à partir des deux autres côtés connus, ou pour vérifier si un triangle est bien rectangle.
Le théorème de Pythagore est donc une notion mathématique clé à connaître pour les élèves qui étudient la géométrie.
Rappel : comment calculer le théorème de pythagore ?
Un triangle rectangle est un triangle qui possède un angle droit : ABC est rectangle en A.
- L’hypoténuse est le côté situé en face de l’angle droit. C’est aussi le côté le plus long.
- Les angles aigus sont complémentaires : ACB et CBA font 90°.
- On rappelle aussi que, dans un triangle quelconque, la somme des trois angles vaut180°
Théorème de Pythagore : formule
Voici Comment bien rédiger le théorème de Pythagore ?
Il a deux façons d’exprimer la formule du théorème de Pythagore :
- Si ABC est un triangle rectangle alors BC² =AB² + AC².
- Ou de façon plus générale :
Dans un triangle rectangle, la somme des carrés des côtés de l’angle droit est égale à l’hypoténuse au carré.
L’égalité BC² =AB² + AC² s’appelle l’égalité de Pythagore.
Attention :
Le théorème de Pythagore ne s’applique qu’aux triangles rectangles.
Dans un triangle rectangle, le théorème de Pythagore permet de calculer la longueur d’un côté connaissant les longueurs des deux autres côtés.
Exemples de théorème de Pythagore :
Exemple 1
ABC est un triangle rectangle en A tel que AB=4cm et AC=3cm. Quelle est la longueur BC ?
Théorème de Pythagore : rédaction
« On donne la configuration » ABC est rectangle en I, on peut appliquer le théorème de Pythagore.
Calculer BC :
On donne l’égalité de Pythagore
ABC est un triangle rectangle en A
Or, d’après le théorème de Pythagore
on a : BC² =AB² + AC²
BC² = 3² + 4²
BC² = 9 + 16
Donc, BC² = 25
BC=√25 « On utilise la touche racine carrée √… »
BC = 5 cm
Le segment [BC] mesure 5 cm
Exemple 2
« On donne la configuration », EFG est un triangle rectangle en F tel que EG=5cm et FG=3cm. Quelle est la longueur EF ?
Rédaction :
On donne l’égalité de Pythagore
EFG est un triangle rectangle en F
Or, d’après le théorème de Pythagore
on a : EG² = FG² + FE²
5² = 3² + FE²
« Attention à cette étape »
FE² = 5² – 3²
FE² = 25 – 9
Donc, FE² = 16
FE=√16 « On utilise la touche racine carrée √… »
FE = 4 cm
Le segment [BC] mesure 4 cm
Démonstration du théorème de pythagore
Pythagore triangle rectangle: propriété pour démontrer qu’un triangle est rectangle
Si le carré de la longueur du plus grand côté d’un triangle est égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle est rectangle.
Exemple :
Le triangle ABC de côtés AB = 6, AC = 8 et BC = 10 est-il rectangle ?
Modèles de rédaction pour le théorème de Pythagore :
BC est le plus grand côté et BC² = 100
AB² + AC² = 100
6² + 8² = 100
Donc BC² = AB² + AC²
Si le carré de la longueur du plus grand côté d’un triangle est égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle est rectangle.
Donc, le triangle ABC est rectangle en A.
Propriété pour démontrer qu’un triangle n’est pas rectangle
Si le carré de la longueur du plus grand côté d’un triangle n’est pas égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle n’est pas rectangle.
Exemple :
Le triangle IJK de côtés IJ = 2, IK = 3 et LK = 4 est-il rectangle ?
Rédaction :
JK est le plus grand côté et JK² = 16
IJ² + IK² = 13
Donc JK² ≠IJ² + IK²
Si le carré de la longueur du plus grand côté d’un triangle n’est pas égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle n’est pas rectangle.
Donc le triangle IJK n’est pas rectangle.
Exercices sur le Pythagore de Pythagore
Le théorème de Pythagore est une formule mathématique qui relie les longueurs des côtés d’un triangle rectangle. Il stipule que pour tout triangle rectangle où la somme des carrés des longueurs de ses jambes est égale au carré de son hypoténuse,
Vous trouverez ci-dessous une liste d’exercices corrigés :
Fiche 1
Cette fiche d’exercices sur le théorème de Pythagore contient huit exercices corrigés de difficulté progressive, accompagnés d’explications détaillées et d’exemples pratiques. Les exercices portent sur des cas concrets et aident les élèves à s’entraîner et à renforcer leurs connaissances en mathématiques..
Fiche 2
Cette fiche d’exercices sur la Propriété de Pythagore comprend trois exercices corrigés avec une difficulté progressive, permettant aux élèves de maîtriser la méthode de calcul de la longueur des côtés en utilisant cette propriété mathématique.
Les exercices sont accompagnés d’exemples concrets, d’explications détaillées et de corrigés pour aider les élèves à consolider leur compréhension de cette propriété importante en mathématiques.
Fiche 3
Cette fiche d’exercices sur le théorème de Pythagore contient un seul exercice corrigé sur la mesure de la distance entre deux points sur un plan en utilisant ce théorème.
L’exercice est accompagné d’explications détaillées, d’un exemple pratique et des corrigés pour aider les élèves à mieux comprendre le concept et à s’entraîner.
Fiche 4
Cette fiche d’exercices sur le théorème de Pythagore comprend plusieurs exercices variés avec des difficultés progressives pour aider les élèves à développer leur compréhension de cette propriété mathématique.
Les exercices portent sur des situations pratiques, accompagnées d’explications détaillées et de corrigés pour permettre aux élèves de vérifier leur travail et de mieux assimiler les notions. Cette fiche est une ressource précieuse pour les élèves cherchant à maîtriser cette notion .
Fiche 5
Cette fiche pour les 4èmes offre des exercices sur le théorème de Pythagore et sa réciproque. Les élèves pratiquent par des calculs de longueurs dans des triangles rectangles et utilisent la réciproque pour identifier ces triangles. Les exercices, avec corrections, aident à renforcer la compréhension de ces principes mathématiques essentiels.
Fiche 6
Cette fiche propose des exercices sur le théorème de Pythagore pour les 4èmes, incluant calculs de longueurs et identification de triangles rectangles. Elle comprend une activité pratique, encourageant l’auto-correction et l’application concrète du théorème.
Fiche 7
Cette fiche propose une série d’exercices corrigés sur le théorème de Pythagore, destinée aux élèves de 4ème. Elle comprend des problèmes variés pour calculer des longueurs dans des triangles rectangles et appliquer la réciproque du théorème. Les exercices vont de la vérification de triangles rectangles à des applications concrètes comme la mesure de distances. Des corrections détaillées accompagnent chaque problème, offrant un outil pratique pour l’auto-évaluation et la consolidation des connaissances en géométrie.
Conclusion
Le théorème de Pythagore établit qu’un triangle rectangle a une relation spécifique entre ses côtés : le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés (a2+b2=c2a2+b2=c2). Sa réciproque permet de déterminer si un triangle est rectangle en vérifiant cette condition. Ces principes sont essentiels en géométrie pour analyser des triangles et résoudre des problèmes spatiaux.

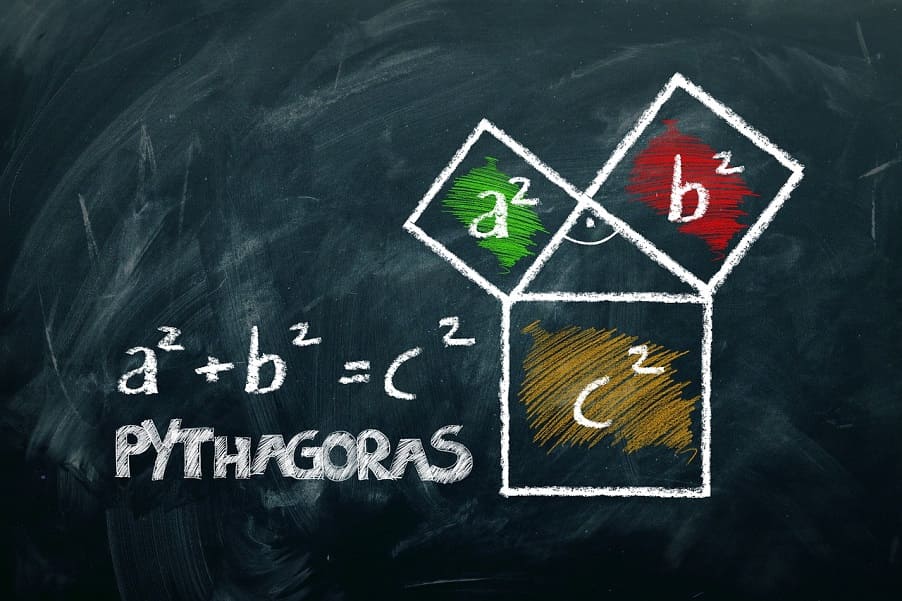
Vraimment c’est intéressant, mais pour bien maitriser-ça, il faut passé par des nombreux exercices, car ce systhème de ce calcul-ici, complique beaucoup de gens.
C’est très génial