Le volume d’une pyramide, c’est l’espace qu’elle prend, un peu comme combien de petites boîtes on pourrait y mettre. Les pyramides peuvent avoir différentes formes de base – un carré, un triangle, ou autre, et leur nom vient de cette forme. Elles ont des côtés en triangle qui se rejoignent en un point au-dessus. Pour savoir combien d’espace prend une pyramide, on utilise une formule spéciale. Voyons comment ça marche avec des exemples simples.
Qu’est-ce que le volume d’une pyramide ?
Le volume d’une pyramide, c’est l’espace à l’intérieur, et il est égal à un tiers de celui d’un prisme avec la même base et la même hauteur. En gros, si on prend trois pyramides identiques, on peut les assembler pour créer un prisme du même type.
Par exemple, avec trois pyramides ayant des bases carrées, on peut former un cube. Voici comment on peut le voir : imaginez remplir une pyramide à base carrée de sable, puis verser ce sable dans un prisme carré de même hauteur. Vous verrez que le prisme peut contenir exactement trois fois le sable de la pyramide.
Comment calculer le volume d’une pyramide ?
Le volume d’une pyramide est égal à un tiers du volume du prisme correspondant (c’est-à-dire que leurs bases et leurs hauteurs sont congruentes).
Formule du volume d’une pyramide :
| Volume de la pyramide = (1/3) × (Aire Base × Hauteur) |
B = Aire de la base de la pyramide
H = Hauteur de la pyramide
Comment calculer le volume des différents types de pyramides ?
Volume d’une pyramide = (1/3) × ( Aire de Base ) × ( Hauteur de la pyramide ).
| Pyramide | volume |
| Pyramide triangulaire | V = 1/3 × B × h V = 1/3 × 1/2 × b × H × h V = 1/6 × B × H × h |
| Pyramide carrée | V = 1/3 × B × h V = 1/3 × a 2 × h |
| Pyramide rectangulaire | V = 1/3 × B × h V = 1/3 × L × l × h |
| Pyramide pentagonale | V = 1/3 × B × h V = 1/3 × 5/2 × c × a × h V = 5/6 × c × a × h |
| Pyramide hexagonale | V = 1/3 × B × h V = 1/3 × 3 × a × c × h V = a × c × h |
1. Volume d’une pyramide à base carrée
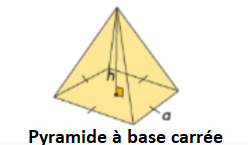
V = 1/3 × B × h
V = 1/3 × a 2 × h
a est la longueur d’un côté de la base carrée et h est la hauteur de la pyramide (la distance verticale du sommet de la pyramide à sa base).
Exemple :
Prenons une pyramide à base carrée avec un côté de la base a=4 cm et une hauteur h=9 cm. Utilisons la formule pour calculer le volume :
V =1/3 × a 2 × h
V =1/3 × 4 2 × 9 cm
V = 1/3 × 16 cm2 × 9 cm
V =1/3 × 144 cm³
V = 144 cm³ : 3
V = 48 cm³
Donc, le volume de la pyramide est de 48 cm³.
2. Volume d’une pyramide à base rectangulaire
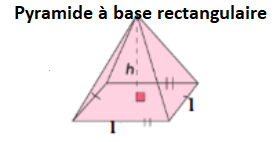
V = 1/3 × B × h
V = 1/3 × L × l × h
Le volume V d’une pyramide à base rectangulaire se calcule avec la formule V = 1/3 × L × l × h, où L est la longueur de la base, l est la largeur de la base, et h est la hauteur de la pyramide (distance verticale du sommet à la base).
Exemple pratique :
Supposons qu’une pyramide à base rectangulaire ait une longueur de base L=6 cm, une largeur de base l = 4 cm, et une hauteur h = 9 cm. Calculons son volume :
V = 1/3 × L × l × h
V = 1/3 × 6 cm × 4 cm × 9 cm
V = 1/3 × 24 cm2 × 9 cm
V = 216 cm3 : 3
V = 72cm3
Donc, le volume de la pyramide est de 72 cm³.
3. Volume d’une pyramide à base triangulaire
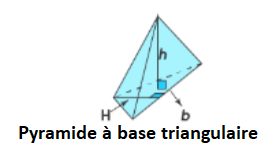
V = 1/3 × B × h
= 1/3 × 1/2 × b × H × h
V = 1/6 × B × H × h
Le volume V d’une pyramide à base triangulaire se calcule avec la formule :
V = 1/6 × B × H × h
Où b est la longueur de la base du triangle, H est la hauteur du triangle (perpendiculaire à la base), et h est la hauteur de la pyramide (la distance verticale du sommet de la pyramide à sa base).
Exemple pratique :
Imaginons une pyramide à base triangulaire dont la base du triangle mesure b=4 cm, la hauteur du triangle H=3 cm, et la hauteur de la pyramide h=9 cm. Utilisons la formule pour calculer le volume :
V = 1/6 × B × H × h
V = 1/6 × 4 cm × 3 cm × 9 cm
= 1/6 × 12 cm2 × 9 cm
V = 1/6 × 108 cm3
V = 18 cm3
Ainsi, le volume de la pyramide est de 18 cm³.
4. Volume d’une pyramide à base hexagonale
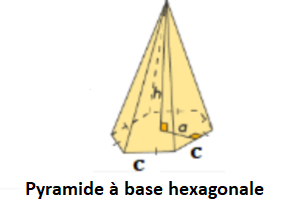
V = 1/3 × B × h
= 1/3 × 3 × a × c × h
V = a × c × h
Pour calculer le volume d’une pyramide à base hexagonale, utilisez la formule :
V = a × c × h
où a est l’apothème de la pyramide, c est la longueur d’un côté de la base, et h est la hauteur de la pyramide.
Pour les cas où les triangles sont équilatéraux et l’apothème n’est pas mentionné, une autre formule est : Volume = (3/2) × a2 × h
où a est la longueur d’un côté de la base et h est la hauteur.
Exemple
Pour une pyramide à base hexagonale avec un côté de 4 cm , une apothème de 5.2 cm, et une hauteur de 10 cm , selon formule :
V = a × c × h
= 4 cm × 5.2 cm × 10 cm
V = 208 cm3.
Volume d’une pyramide : exercices avec corrigé à imprimer
Voici des fiches d’exercices pour vous aider à appliquer cette notion mathématique :
Fiche 1
Ce fichier propose des exercices sur le calcul du volume de pyramides, en se concentrant notamment sur une boîte de chocolat en forme de tronc de pyramide. Les exercices demandent de calculer le volume de pyramides régulières avec des bases spécifiques (carrée et autres), d’identifier des coefficients de réduction entre différentes pyramides, et de déduire des volumes en fonction de ces coefficients.
Fiche 2
Ce fichier est un ensemble d’exercices sur les pyramides et les cônes destinés à des élèves de 4ème. Il contient des activités variées comme la réalisation de dessins en perspective de pyramides et de cônes, l’identification de patrons corrects de pyramides, et des calculs de volumes pour différentes formes géométriques, y compris des pyramides à base carrée, rectangulaire, et des cônes.
Fiche 3
Le présent fichier contient une série d’exercices corrigés sur les pyramides et les cônes, destinés à des élèves de niveau collège. Il inclut des exercices sur le vocabulaire spécifique aux pyramides et aux cônes, la représentation et la construction de ces formes géométriques, ainsi que des problèmes mathématiques nécessitant le calcul de volumes.
Fiche 4
Ce document contient des exercices de mathématiques pour des élèves de 4ème, se concentrant sur les volumes de différentes formes géométriques, notamment des pyramides et des cônes. Les tâches vont du calcul de volumes de solides basés sur des dimensions données à des questions plus complexes impliquant des formules spécifiques pour chaque type de forme. Les exercices sont accompagnés de corrigés détaillés, permettant aux élèves de vérifier leurs réponses et de comprendre les étapes de résolution.
Lire aussi :
- Comment calculer l’aire d’un rectangle ?
- Comment calculer l’aire d’un carré ?
- Comment calculer l’aire d’un triangle ?

Vous êtes très intéressant
Oups, erreur dans la formule du volume de la pyramide à base rectangulaire (dans le tableau) : V est bien = 1/3 x B x h = 1/3 x L x l x h = 1/3 x Llh (pas 1/6 Llh). Formule V = 1/3 x Llh correctement utilisée dans l’Exemple 3.