Le volume d’un prisme est la capacité du prisme. Il peut y avoir différents types de prismes tels qu’un prisme triangulaire, un prisme carré, un prisme rectangulaire, un prisme pentagonal, un prisme hexagonal ou un prisme octogonal. Mais la méthode pour écrire la formule du volume de n’importe quel prisme reste la même, indépendamment du type de prisme. Le concept d’écriture de la formule pour le volume du prisme reste le même dans tous les cas. Comme pour toutes les formes tridimensionnelles, vous apprendrez à calculer le volume de n’importe quel type de prisme. Restez à l’écoute pour apprendre comment calculer le volume d’un prisme droit à l’aide d’exemples résolus.
Qu’est-ce que le volume d’un prisme ?
Le volume d’un prisme est défini comme la quantité d’espace occupée par un prisme. Un prisme est une forme solide en 3D qui possède deux faces identiques et d’autres faces qui ressemblent à un parallélogramme. C’est un polyèdre dont la convention de nommage est influencée par les différentes formes des bases.
Dans le cas des prismes, chaque prisme a une base différente, un prisme triangulaire (base triangulaire), un prisme carré (base carrée), un prisme rectangulaire (base rectangulaire), un prisme pentagonal (base pentagonale), un prisme hexagonal (base hexagonale) ou un prisme octogonal (base octogonale). Ainsi, comme chaque prisme est une forme tridimensionnelle, le volume de chaque prisme se situe également dans un plan tridimensionnel.
L’unité de volume d’un prisme est donnée en mètres cubes, centimètres cubes, pouces cubes ou pieds cubes, etc.
Formule de volume d’un prisme droit
La formule du volume d’un prisme est donnée par le produit de l’aire de la base et de la hauteur du prisme.
| V = B × H Volume prisme droit = l’aire de la base × la hauteur du prisme |
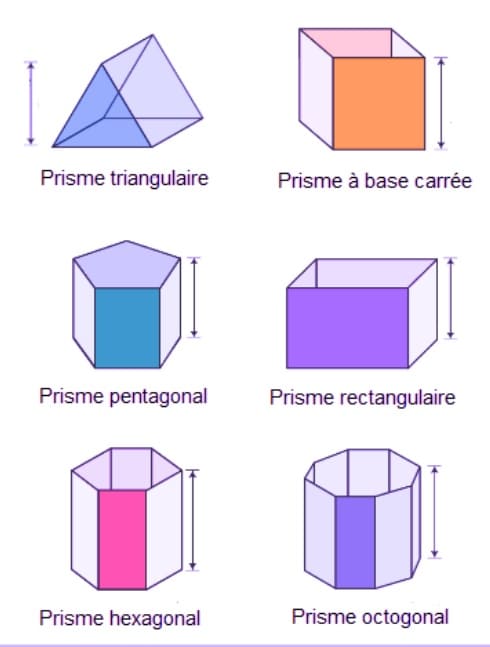
Ainsi, comme les bases de différents types de prismes sont différentes, les formules pour déterminer le volume du prisme le sont également. Regardez le tableau ci-dessous pour comprendre ce concept plus en détail :
| Forme de Prismes | Base | Formule de volume |
|---|---|---|
| Prismes triangulaires | Triangle | Volume du prisme triangulaire = Aire du triangle × hauteur du prisme |
| Prismes carrés | Carré | Volume du prisme carré = Aire du carré × hauteur du prisme |
| Prismes rectangulaires | Rectangle | Volume du prisme rectangulaire = Aire du rectangle × hauteur du prisme |
| Prismes trapézoïdaux | Trapézoïde | Volume du prisme trapézoïdal = Aire du trapézoïde × hauteur du prisme |
| Prismes pentagonaux | Pentagone | Volume du prisme pentagonal = Aire du pentagone × hauteur du prisme |
| Prismes hexagonaux | Hexagone | Volume du prisme hexagonal = Aire de l’hexagone × hauteur du prisme |
| Prismes octogonaux | Octogone | Volume du prisme octogonal = Aire de l’octogone × hauteur du prisme |
Ainsi, le volume d’un prisme peut être exprimé comme V = B × H où V est le volume, B l’aire de la base et H la hauteur du prisme. L’unité de l’aire de base est exprimée en unités carrées et la hauteur du prisme est exprimée en unités de longueur. Par conséquent, l’unité de volume du prisme est donnée comme V = (unités carrées) × (unités de longueur) = unités cubes.
Comment calculer le volume d’un prisme ?
Les étapes pour déterminer le volume d’un prisme sont les suivantes :
- Étape 1 :
Écrire les dimensions données du prisme.
- Étape 2 :
Déterminer le volume du prisme en utilisant la formule V = B × H où V, B et H sont respectivement le volume, l’aire de la base et la hauteur du prisme.
- Étape 3 :
Une fois la valeur du volume du prisme obtenue, ajouter l’unité de volume du prisme à la fin (en unités cubes).
Exemples
Exemple 1
Trouver le volume d’un prisme dont l’aire de la base est de 3 centimètres carrés et la hauteur est de 7 centimètres.
Solution
- Comme nous le savons, le volume du prisme est V = B × H.
- Étant donné que : B = 3 centimètres carrés,
- H = 7 centimètres Ainsi, le volume du prisme,
- V = B × H ⇒ V = 3 × 7 = 21 cm 3
- Par conséquent, le volume du prisme est de 21 pouces cubes.
Notes importantes
Le volume de tout prisme dépend de la forme de sa base. Avec le changement de forme de la base, l’aire de la base change également.
Exemple 2
Quelle est l’aire de la base du prisme si le volume du prisme est de 324 centimètres cubes et la hauteur du prisme est de 9 centimètres ?
Solution
- Les dimensions données sont :
- le volume du prisme = 324 centimètres cubes
- et la hauteur du prisme = 9 centimètres.
- Soit « B » l’aire de la base du prisme.
- En substituant les valeurs dans la formule du volume du prisme,
- Volume du prisme = V = B × H = 324 unités cubes
- ⇒ 9B = 324
- ⇒ B = 36 centimètres carrées
- Par conséquent, l’aire de la base du prisme est de 36 centimètres carrés.
Exemple 3
Trouver la hauteur du prisme si le volume du prisme est de 729 centimètres cubes et l’aire de la base est de 27 centimètres carrés.
Solution :
- Les dimensions données sont :
- le volume du prisme = 729 centimètres cubes
- et l’aire de la base du prisme = 27 centimètres carrés.
- Soit « H » la hauteur du prisme.
- En substituant les valeurs dans la formule du volume du prisme,
- Volume du prisme = V = B × H = 729 centimètres cubes
- ⇒ 27H = 729
- ⇒ H = 27 centimètres
- Par conséquent, la hauteur du prisme est de 27 centimètres.
Lire aussi
- Comment calculer le volume d’une pyramide ?
- Comment calculer le volume d’un cône ?
- Comment calculer le volume d’un cube ?
Laisser un commentaire