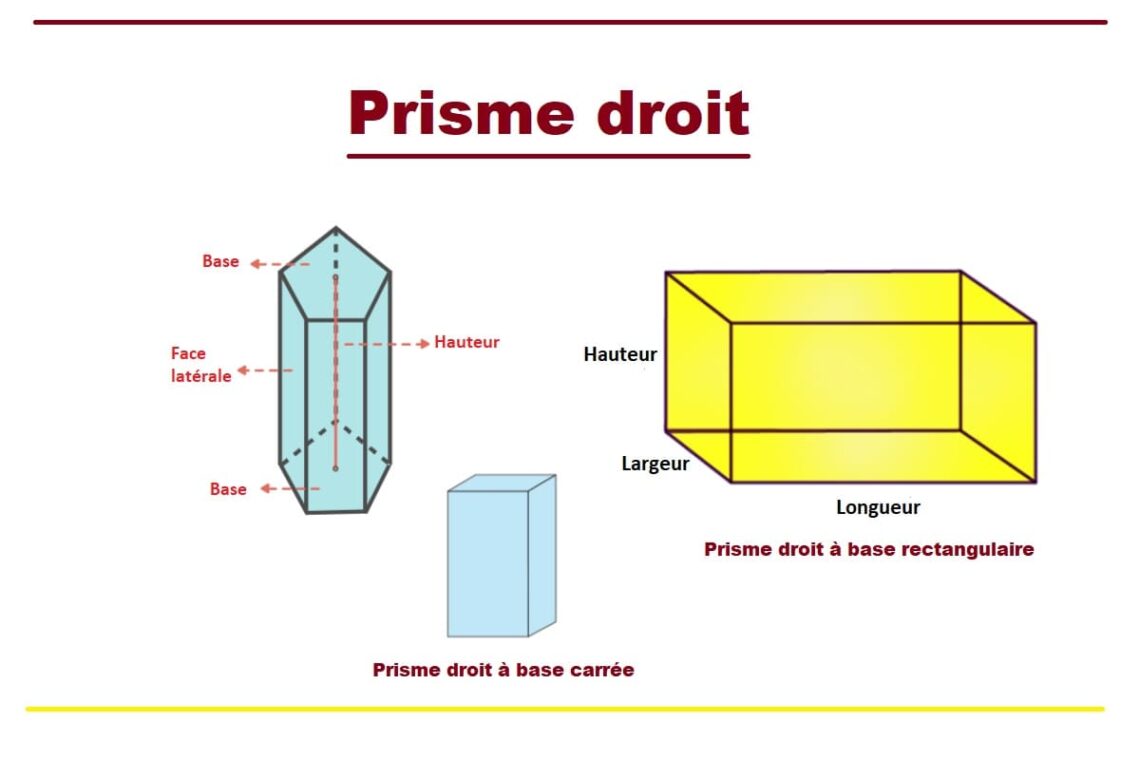
Le prisme droit est une forme à trois dimensions avec deux faces identiques et parallèles appelées bases. Les côtés du prisme sont des formes en parallélogramme.
Définition
Le prisme droit est une forme géométrique dont les côtés sont rectangles ou carrés. Cela inclut les prismes avec des formes régulières (où tous les côtés sont identiques) et ceux avec des formes irrégulières (où les côtés peuvent varier).
En gros, si un prisme a des côtés droits formant des rectangles ou des carrés, on l’appelle un prisme droit, que sa forme soit régulière ou non.
Formule de volume prisme droit
Pour expliquer de manière simple aux élèves de collège, imaginons que vous ayez une boîte de forme rectangulaire. Pour trouver combien elle peut contenir, vous devez calculer son volume.
La formule pour le volume d’un prisme droit est :
| Volume = Aire de la base × Hauteur |
Voici quelques exemples pour illustrer comment calculer le volume d’un prisme droit :
Volume prisme droit à base rectangulaire
Supposons que la base de la boîte soit un rectangle de 4 cm de long et 3 cm de large. La hauteur de la boîte est de 6 cm.
- Calculez d’abord l’aire de la base :
Aire = Longueur × Largeur
= 4 cm × 3 cm = 12 cm².
- Ensuite, multipliez cette aire par la hauteur du prisme :
- Volume = Aire de la base × Hauteur
= 12 cm² × 6 cm
Volume = 72 cm³.
Donc, le volume de la boîte est de 72 cm³.
Volume prisme droit à base carrée
- Côté du carré de la base : 4 cm
- Hauteur du prisme : 10 cm
- Volume = Côté² × Hauteur = 4 cm × 4 cm × 10 cm = 160 cm³
Volume prisme droit à base hexagonale
- Côté de l’hexagone : 2 cm (hexagone régulier)
- Hauteur du prisme : 7 cm
- Aire de la base (hexagone) = (3√3/2) × Côté² = (3√3/2) × (2 cm)² ≈ 10.39 cm²
- Volume = Aire de la base × Hauteur ≈ 10.39 cm² × 7 cm ≈ 72.73 cm³
Le volume de prisme droit à base pentagonale
- Côté du pentagone : 3 cm (pentagone régulier)
- Hauteur du prisme : 6 cm
- Aire de la base (pentagone) = (5/4) × Côté² × cot(π/5) ≈ 15.48 cm²
- Volume = Aire de la base × Hauteur ≈ 15.48 cm² × 6 cm ≈ 92.88 cm³
Volume prisme droit à base de parallélogramme
- Base = 5 cm, Hauteur du parallélogramme = 4 cm
- Hauteur du prisme : 9 cm
- Aire de la base = Base × Hauteur du parallélogramme = 5 cm × 4 cm = 20 cm²
- Volume = Aire de la base × Hauteur = 20 cm² × 9 cm = 180 cm³
Volume prisme droit à base octogonale
- Côté de l’octogone : 2 cm (octogone régulier)
- Hauteur du prisme : 5 cm
- Aire de la base (octogone) = 2(1 + √2) × Côté² ≈ 19.31 cm²
- Volume = Aire de la base × Hauteur ≈ 19.31 cm² × 5 cm ≈ 96.55 cm³
Le volume de prisme droit à base quadrilatère
- Pour un quadrilatère quelconque, prenons un rectangle : Longueur = 6 cm, Largeur = 4 cm
- Hauteur du prisme : 7 cm
- Volume = Longueur × Largeur × Hauteur = 6 cm × 4 cm × 7 cm = 168 cm³
Volume prisme droit à base losange
- Diagonales du losange : d1 = 8 cm, d2 = 6 cm
- Hauteur du prisme : 5 cm
- Aire de la base = (d1 × d2) / 2 = (8 cm × 6 cm) / 2 = 24 cm²
- Volume = Aire de la base × Hauteur = 24 cm² × 5 cm = 120 cm³
Voir aussi : Comment calculer l’aire d’un prisme droit ?
Comment calculer la base d’un prisme droit ?
Pour calculer l’aire de la base d’un prisme droit si vous connaissez déjà son volume et sa hauteur, vous pouvez utiliser la formule générale du volume et la réarranger. La formule de base est :
Volume = Aire de la base × Hauteur
En réarrangeant cette formule pour trouver l’aire de la base, vous obtenez :
Aire de la base = Volume : Hauteur
Voici un exemple pour illustrer cette méthode :
Exemple : Supposons que vous ayez un prisme droit avec un volume de 150 cm³ et une hauteur de 10 cm. Pour trouver l’aire de la base, vous ferez le calcul suivant :
Aire de la base = Volume : Hauteur
=150 cm³ : 10 cm
=15 cm²
Ainsi, l’aire de la base du prisme est de 15 cm².
Comment calculer la hauteur d’un prisme droit ?
Pour calculer la hauteur d’un prisme droit lorsque vous connaissez son volume et l’aire de sa base, vous pouvez réarranger la formule initiale.
Volume = Aire de la base × Hauteur
Pour trouver la hauteur, réarranger cette formule comme suit :
Hauteur = Volume : Aire de la base
Exemple :
Imaginons que vous avez un prisme droit avec un volume de 200 cm³ et une base dont l’aire est de 20 cm². Pour trouver la hauteur du prisme, faites le calcul suivant :
Hauteur = Volume : Aire de la base
= 200 cm³ : 20 cm²
= 10 cm
Donc, la hauteur du prisme est de 10 cm.
Exercices corrigés
Exercice 1
Emma veut faire une boîte sans couvercle. Ses dimensions sont : 7 mètres de long, 5 mètres de large et 9 mètres de haut. Pour savoir combien de cartons elle doit acheter, elle calcule la surface de la boîte.
Voici comment :
- Fond de la boîte (longueur x largeur) : 7 x 5 = 35 mètres carrés
- Côtés (deux fois hauteur x largeur) : 2 x 9 x 5 = 90 mètres carrés
- Devant et derrière (deux fois hauteur x longueur) : 2 x 9 x 7 = 126 mètres carrés
Elle additionne tout : 35 + 90 + 126 = 251 mètres carrés.
Donc, Emma a besoin de 251 mètres carrés de carton.
Exercice 2
Énoncé : Un prisme droit a pour base un rectangle de dimensions 5 cm et 3 cm. La hauteur du prisme est de 10 cm. Calculez le volume du prisme.
Solution :
Volume = Longueur × Largeur × Hauteur
= 5 cm × 3 cm × 10 cm
= 150 cm³
Exercice 3
Énoncé : Un prisme droit a une base carrée de côté 4 cm et une hauteur de 6 cm. Calculez l’aire totale de la surface du prisme.
Solution :
Aire de la base = côté × côté
= 4 cm × 4 cm
= 16 cm²
Aire latérale = Périmètre de la base × Hauteur
= 4 côtés × 4 cm × 6 cm
= 96 cm²
Aire totale = 2 × Aire de la base + Aire latérale
= 2 × 16 cm² + 96 cm²
= 128 cm²
Exercice 4
Énoncé : Un prisme droit a pour base un triangle rectangle avec des côtés de 3 cm et 4 cm. Le volume du prisme est de 60 cm³. Trouvez la hauteur du prisme.
Solution :
Aire de la base = (Côté 1 × Côté 2) / 2
= (3 cm × 4 cm) / 2
= 6 cm²
Volume = Aire de la base × Hauteur.
= 6 cm² × Hauteur
= 60 cm³ / 6 cm²
Volume = 10 cm

Laisser un commentaire