Pour savoir combien d’espace prend un pavé droit, ou calculer le volume d’un pavé droit, il suffit de multiplier ensemble sa longueur, sa largeur et sa hauteur. C’est une méthode simple et pratique, utile au quotidien comme en maths. Nous allons voir comment faire ce calcul facilement, pour que tout le monde puisse le comprendre et l’utiliser.
Qu’est ce qu’un pavé droit ?
Un pavé droit, également connu sous le nom de parallélépipède rectangle, est une forme géométrique tridimensionnelle définie par six faces rectangulaires. Il s’agit d’un type de parallélépipède dont les trois angles formés par les arêtes issus d’un sommet sont droits, ce qui signifie que tous les angles du pavé droit sont droits. Les faces opposées de cette forme sont égales, ce qui caractérise davantage sa géométrie régulière et son alignement perpendiculaire.
Formule du volume d’un pavé droit :
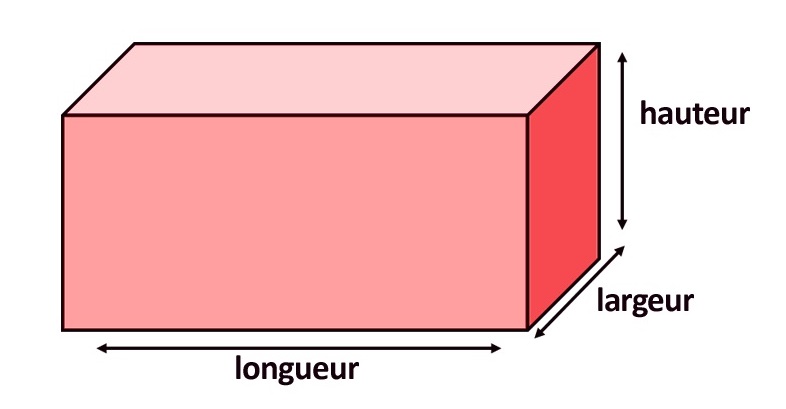
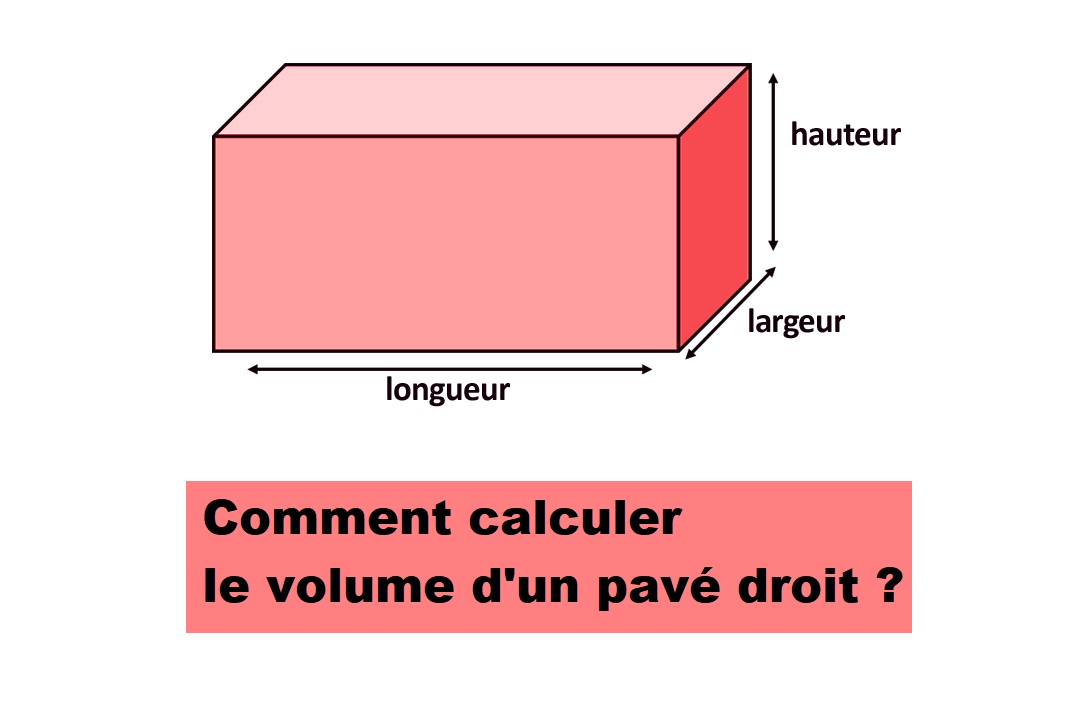
Pour calculer le volume d’un pavé droit, multipliez simplement sa longueur par sa largeur et par sa hauteur.
Volume d’un pavé droit = Longueur × largeur × hauteur.
| V = L × l × h |
- L = Longueur
- l = largeur
- h = hauteur
Volume d’un pavé droit à base carrée
Pour calculer le volume d’un pavé droit à base carrée, la méthode est directe et se base sur une formule simple. Étant donné que la base du pavé droit est carrée, l’aire B de cette base est le carré de la longueur du côté du carré, soit c×c.
L’aire de base (B) = c×c
Le volume V du pavé droit est alors calculé en multipliant l’aire de la base par la hauteur h du pavé droit. Ainsi, la formule pour calculer le volume V devient V = B × h = c × c × h, où cc est la longueur du côté de la base carrée et h est la hauteur du pavé droit.
Formule du volume d’un pavé droit à base carré :
| V = C × C × H |
- C = 5 cm (la longueur du côté à base carrée)
- H = 8 cm (la hauteur du pavé droit)
En substituant ces valeurs dans la formule, nous obtenons :
V = C × C × H
= 5 cm × 5 cm × 8 cm
V = 200 cm3
Donc, le volume de la boîte est de 200 cm3. Cela signifie que la boîte peut contenir un volume jusqu’à 200 centimètres cubes d’espace à l’intérieur.
Volume d’un pavé droit coupé en diagonale
Pour comprendre le volume d’un pavé droit coupé en diagonale, il faut d’abord connaître le volume d’un pavé droit, qui se calcule en multipliant ses trois dimensions : longueur, largeur, et hauteur, avec la formule :
V = L × l × H
La longueur de la diagonale d’un pavé droit, qui relie deux sommets opposés, se trouve avec :
| D = √ a2 + b2 + c2 |
Si on coupe un pavé droit en suivant une de ses diagonales, cela nous donne deux nouvelles formes géométriques. Le calcul de leur volume ne serait pas direct, car cela dépendrait exactement de comment et où la coupe est faite. Pour des calculs plus précis, on aurait besoin de détails spécifiques sur ces nouvelles formes.
Pour des pavés droits standards, les calculs sont assez droits grâce aux formules données. Mais pour des formes obtenues après une coupe diagonale, cela pourrait nécessiter des techniques mathématiques plus avancées, peut-être spécifiques à chaque cas.
Exemple :
- Longueur (L) = 4 cm
- Largeur (l) = 3 cm
- Hauteur (H) = 2 cm
Pour calculer le volume de ce pavé droit, nous utiliserons la formule
V = L × l × H
En substituant les valeurs données, nous obtenons :
V = 4 cm × 3 cm × 2 cm
= 24 cm3
Le volume de ce pavé droit est donc de 24 cm3.
Ensuite, si on cherche à connaître la longueur de la diagonale de ce pavé droit, on utilise la formule :
D = √ a2 + b2 + c2
. En remplaçant par les valeurs données :
D = √ 16 cm + 9 cm + 4 cm
= √29 cm
La longueur de la diagonale de ce pavé droit est donc √ 29 cm, ce qui est environ 5,39 cm après calcul.
Volume d’un pavé droit : exercices avec corrigé
Exercice de base
Problème :
Calculer le volume d’un pavé droit dont les dimensions sont 4 cm de longueur, 3 cm de largeur, et 2 cm de hauteur.
Solution :
Utilisons la formule du volume pour un pavé droit,
V= longueur × largeur × hauteur
V = 4 cm × 3 cm × 2 cm
= 24 cm³
Réponse :
Le volume du pavé droit est de 24 cm³.
Exercice appliqué
Problème :
Vous souhaitez creuser une piscine rectangulaire de 9 mètres de long et 12 mètres de large. Quelle profondeur doit-elle avoir pour obtenir un volume de 189 mètres cubes ?
Solution :
La formule du volume est:
V=longueur×largeur×hauteur
donc la hauteur (profondeur) peut être trouvée par :
Hauteur= Volume : ( longueur×largeur )
Hauteur = 189 m³ : ( 9 m ×12 m )
Hauteur = 189 m³ : 108 m²
Réponse :
La piscine doit être creusée à une profondeur de 1,75 mètre.
Exercice de compréhension
Problème :
Une pièce en forme de pavé droit a un volume de 21,84 m³ et l’aire de son sol est de 8,4 m². Si la longueur de la pièce est de 3,5 m, pouvez-vous trouver sa largeur ?
Solution :
Sachant que
Volume = longueur×largeur×hauteur
et que Aire de base=longueur×largeur, nous pouvons trouver la largeur si nous organisons la formule de l’aire de la base :
Largeur = Aire de base : longueur.
L’aire de la base est donnée et équivaut au sol de la pièce, donc Aire base=8,4 m2. La longueur est de 3,5 m.
Largeur = 8,4 m² : 3,5 m
=2,4 m
Réponse :
La largeur de la pièce est de 2,4 mètres.
Exercices sur l’aire d’un prisme droit 6ème à imprimer
Voici des exercices en format de PDF sur le prisme droit :
Fichier 1
Le fichier est un ensemble d’exercices de mathématiques pour les élèves de 5ème, centré sur le prisme droit. Il propose des activités variées, telles que reconnaître les faces parallèles et perpendiculaires, dessiner des prismes en perspective, calculer des volumes d’objets du quotidien comme des aquariums ou des tentes, et déterminer le volume de béton nécessaire pour des marches. C’est un outil complet pour aborder la géométrie spatiale de manière pratique et théorique.
Fichier 2
Le document explore les concepts des prismes et des cylindres, offrant des définitions claires, des méthodes pour dessiner leurs patrons, et des explications pour calculer leur aire latérale et volume. Il propose des instructions étape par étape, accompagnées de vidéos explicatives, pour aider à la compréhension et à la réalisation des exercices pratiques. Un exemple intéressant inclut le calcul du volume d’un prisme à base triangulaire et d’un cylindre, rendant le contenu accessible et engageant pour les élèves.
Fichier 3
Ce document est un cours de mathématiques pour les élèves de 5ème, axé sur les solides comme les prismes droits et les cylindres. Il commence par introduire les activités à faire, suivi d’une section théorique sur les prismes droits, incluant leur définition, représentation en perspective, et les patrons. Il couvre également les cylindres de révolution, en expliquant leur structure et comment représenter et déplier leur surface latérale. Le document est complété par des exercices pratiques sur le périmètre et l’aire des disques, ainsi que sur les conversions de volumes et contenances, pour renforcer la compréhension de ces concepts.
Fichier 4
Ce fichier contient une série d’exercices sur les prismes droits, visant à approfondir la compréhension des élèves sur la géométrie des solides. Les exercices proposent de déterminer la nature des bases des prismes, calculer leur hauteur, aire latérale et volume. Un tableau à compléter offre une pratique sur la relation entre l’aire de la base, la hauteur, et le volume de différents prismes. Des problèmes pratiques invitent les élèves à appliquer ces concepts dans des contextes variés, renforçant ainsi leur maîtrise du sujet.
Voir aussi :

Laisser un commentaire