La masse volumique est une propriété importante des matériaux. Elle permet de savoir si un objet va flotter ou couler dans l’eau, ou encore d’identifier un métal inconnu. Savoir comment calculer une masse volumique est donc très utile en physique-chimie.
Dans cette fiche, tu vas apprendre la définition de cette notion, découvrir la formule pour la calculer, et voir comment l’utiliser dans différentes situations. Tu verras aussi comment passer d’une unité à une autre, par exemple des g/cm³ aux kg/m³.
Définition et formule de la masse volumique
La masse volumique indique combien pèse un certain volume de matière. Par exemple, un litre d’eau ne pèse pas la même chose qu’un litre d’huile ou qu’un litre de mercure. C’est la masse volumique qui explique cette différence.
La formule de la masse volumique est simple :
ρ = m / V
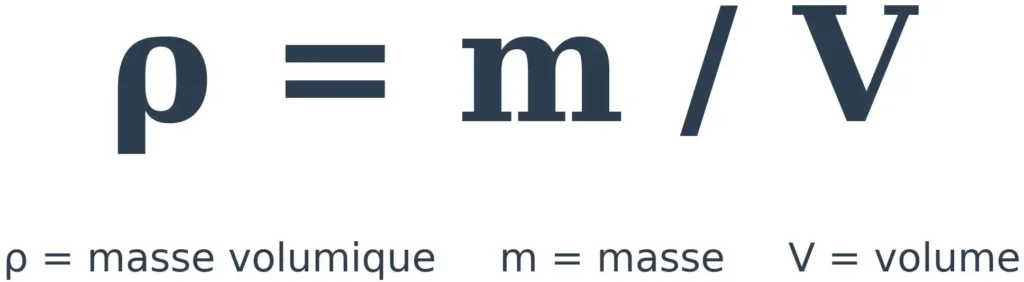
Dans cette formule :
- ρ (la lettre grecque « rhô ») représente la masse volumique
- m est la masse de l’objet
- V est son volume
Les unités les plus utilisées sont le gramme par centimètre cube (g/cm³) et le kilogramme par mètre cube (kg/m³). L’eau a une masse volumique d’environ 1 g/cm³. Cela veut dire qu’un centimètre cube d’eau pèse un gramme.
À retenir
La masse volumique est différente de la densité. La densité compare la masse volumique d’un matériau avec celle de l’eau. Un matériau qui a une masse volumique de 2 g/cm³ a une densité de 2 : il est deux fois plus lourd que l’eau pour le même volume.
Méthode de calcul de la masse volumique
Pour calculer la masse volumique, tu as besoin de deux choses : la masse et le volume de ton échantillon. Ensuite, tu appliques simplement la formule.
Voici un exemple :
Tu as un cube en métal. En le pesant, tu constates qu’il fait 216 grammes. Chaque arête mesure 3 centimètres après mesure. Pour trouver le volume du cube, tu fais 3 × 3 × 3 = 27 cm³.
Maintenant, tu divises la masse par le volume : 216 ÷ 27 = 8 g/cm³. La masse volumique de ce cube est donc de 8 g/cm³. En regardant dans un tableau, tu verras que c’est probablement du laiton ou du cuivre.
Attention
Fais bien attention aux unités. Si tu utilises des grammes et des centimètres cubes, ton résultat sera en g/cm³. Si tu utilises des kilogrammes et des mètres cubes, ton résultat sera en kg/m³. Ne mélange jamais les unités, sinon ton calcul sera faux.
Pour mesurer le volume d’un objet avec une forme irrégulière, tu peux utiliser un récipient gradué avec de l’eau. Tu plonges l’objet dedans et tu regardes de combien le niveau d’eau monte. Cette différence te donne le volume de l’objet.
Calculer un volume à partir de la masse volumique
Maintenant que tu sais calculer une masse volumique, voyons comment faire le calcul inverse. Parfois, tu connais la masse volumique d’un matériau et sa masse, et tu veux trouver son volume.
Pour cela, tu transformes la formule de départ. Si ρ = m / V, alors en réarrangeant les termes, tu obtiens :
V = m / ρ
Autrement dit, le volume est égal à la masse divisée par la masse volumique.
Prenons un exemple concret. Imaginons que tu as un lingot d’or qui pèse 193 grammes. Tu sais que la masse volumique de l’or est de 19,3 g/cm³. Pour trouver le volume de ce lingot, tu fais : 193 ÷ 19,3 = 10 cm³. Ton lingot occupe donc un volume de 10 centimètres cubes.
Astuce
Pour vérifier que ton calcul est correct, tu peux faire une vérification rapide. Reprends ta formule de départ et recalcule la masse volumique avec les valeurs que tu as trouvées. Si tu retombes sur 19,3 g/cm³, c’est bon signe. Cette méthode de vérification fonctionne pour tous les calculs de ce type.
Calculer une masse avec la masse volumique
Tu peux aussi utiliser la masse volumique pour calculer une masse quand tu connais le volume. La formule transformée devient :
m = ρ × V
La masse est égale à la masse volumique multipliée par le volume.
Voici un exemple pratique. Tu remplis une bouteille de 2 litres avec de l’eau. Tu veux savoir combien elle pèse. La masse volumique de l’eau est de 1 g/cm³. Attention, 2 litres correspondent à 2000 cm³. Tu multiplies donc : 1 × 2000 = 2000 grammes, soit 2 kilogrammes. Ta bouteille d’eau pèse 2 kg.
Ce type de calcul est très utile dans la vie quotidienne. Par exemple, si tu veux savoir combien pèse un aquarium plein d’eau, ou si tu dois calculer la charge d’un camion transportant du sable, tu utilises exactement cette méthode.
Il est bon de savoir que cette formule fonctionne pour tous les matériaux. Si tu connais la masse volumique du béton (environ 2,3 g/cm³), tu peux calculer combien pèse une dalle de béton en connaissant son volume. C’est ainsi que les ingénieurs calculent les charges dans la construction.
Conversions d’unités (g/cm³, kg/m³)
Les deux unités principales pour la masse volumique sont le g/cm³ et le kg/m³. Il faut savoir passer de l’une à l’autre, car les exercices et les tableaux n’utilisent pas toujours la même unité.
La règle de conversion est simple à retenir :
1 g/cm³ = 1000 kg/m³
Pour convertir des g/cm³ en kg/m³, tu multiplies par 1000. Pour faire l’inverse (kg/m³ vers g/cm³), tu divises par 1000.
Quelques exemples pour bien comprendre :
- L’eau : 1 g/cm³ = 1000 kg/m³
- Le fer : 7,87 g/cm³ = 7870 kg/m³
- L’aluminium : 2,7 g/cm³ = 2700 kg/m³
Attention
Une erreur fréquente est de multiplier par 100 au lieu de 1000. Fais bien attention à ce piège. Le facteur de conversion est 1000, pas 100. Cette erreur vient souvent du fait qu’il y a 100 centimètres dans un mètre. Mais pour les volumes, on travaille en trois dimensions : il faut donc 100 × 100 × 100 = 1 000 000 de cm³ dans un m³. Avec la conversion des masses (1 kg = 1000 g), on arrive au facteur 1000.
Voici un tableau pour t’aider :
| Matériau | Masse volumique en g/cm³ | Masse volumique en kg/m³ |
| Eau | 1 | 1000 |
| Aluminium | 2,7 | 2700 |
| Fer | 7,87 | 7870 |
| Cuivre | 8,96 | 8960 |
| Plomb | 11,3 | 11 300 |
| Or | 19,3 | 19 300 |
Applications et exercices
La masse volumique est utilisée dans de nombreuses situations pratiques. En chimie, elle permet d’identifier des substances inconnues. En géologie, elle aide à reconnaître les minéraux. Dans l’industrie, elle sert à contrôler la qualité des matériaux.
Voici quelques exercices pour t’entraîner. Un morceau de bois de 500 cm³ pèse 350 grammes. Quelle est sa masse volumique ? Tu appliques la formule : 350 ÷ 500 = 0,7 g/cm³. C’est cohérent avec les bois légers comme le pin ou le sapin.
Autre exemple : tu veux remplir une piscine de 20 m³ avec de l’eau. Combien cela va-t-il peser ? La masse volumique de l’eau est 1000 kg/m³. Tu calcules : 1000 × 20 = 20 000 kg, soit 20 tonnes. Cela montre pourquoi les piscines doivent être bien construites.
Pour se valider, on peut toujours vérifier que les unités sont cohérentes. Si tu divises des grammes par des centimètres cubes, tu dois obtenir des g/cm³. Si tu multiplies des kg/m³ par des m³, tu obtiens des kilogrammes. Cette vérification dimensionnelle est un réflexe à prendre en physique.
Pour approfondir
La masse volumique est étroitement liée au calcul des volumes. Pour aller plus loin dans ta maîtrise de cette notion, voici des ressources complémentaires qui t’aideront à calculer les volumes de différentes formes géométriques.
Calcul de volumes des solides
- Comment calculer le volume d’un cube ? – La forme la plus simple pour débuter
- Comment calculer le volume d’un pavé droit ? – Essentiel pour de nombreux calculs pratiques
- Comment calculer le volume d’un prisme droit ? – Méthode détaillée avec exercices
- Comment calculer le volume d’une pyramide ? – Pour les solides à base triangulaire
- Comment calculer le volume d’un cône ? – Formule et applications pratiques
