Dans l’univers fascinant des nombres, « décomposer » est un mot magique. Il évoque l’idée de séparer, de diviser, un peu comme un magicien qui coupe un objet en plusieurs morceaux. C’est un art que l’on peut appliquer aussi bien aux nombres qu’aux formes géométriques. Quand il s’agit de nombres, décomposer signifie transformer un grand nombre en plusieurs petits.
Prenons un exemple ludique : le nombre 10. C’est comme un puzzle que l’on peut assembler de diverses manières. On peut le décomposer en 5, 3, et 2, ou pourquoi pas en 5, 4, et 1. Il y a toujours plusieurs chemins pour arriver au même résultat.
Les fractions, ces petites parts d’un tout, ne dérogent pas à cette règle. Elles aussi peuvent être décomposées et recomposées, tout comme les nombres entiers. N’est-ce pas fascinant ? Plongeons ensemble dans l’aventure et découvrons les secrets de la décomposition des fractions.
Qu’est ce que la division des fractions ?
Imaginez une fraction comme un gâteau partagé en plusieurs morceaux. Décomposer une fraction, c’est comme diviser ce gâteau en parts encore plus petites. Chaque petit morceau représente une part de la fraction originale, et si on les rassemble tous, on retrouve notre gâteau initial, ou notre fraction de départ.
Prenons un exemple concret : la fraction ¾. Elle nous dit que nous avons trois parts d’un gâteau coupé en quatre. Mais attendez, il y en a plus ! On peut diviser ces parts en morceaux encore plus fins. Ainsi, en jouant avec ces morceaux, on explore la richesse cachée dans chaque fraction.
Quand on décompose une fraction comme 3443 en trois quarts, on la partage en trois fractions plus petites qui, lorsqu’elles sont additionnées, donnent la fraction de départ.
La décomposition est flexible ; elle permet de partager le numérateur en plusieurs morceaux qui ne sont pas forcément égaux, contrairement à la partition où l’on divise en parts égales.
Cette méthode ouvre la porte à une multitude de combinaisons possibles pour explorer les fractions, enrichissant ainsi notre compréhension des nombres et de leurs relations.
Comment décomposer une fraction ?
La décomposition de fractions en fractions unitaires consiste à exprimer une fraction comme la somme de plusieurs fractions ayant chacune un numérateur de 1. Les fractions unitaires représentent une partie d’un tout divisé en parties égales. Par exemple, ½ , ⅓ , ¼ sont toutes des fractions unitaires.
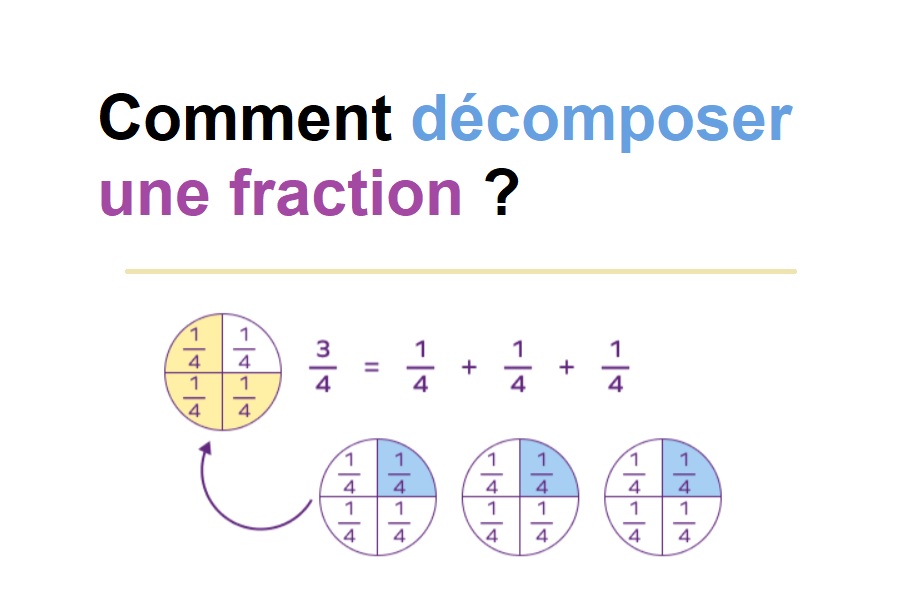
Pour décomposer une fraction comme 3/4 en fractions unitaires, on peut l’écrire comme la somme de trois fractions :
3/4 = 1/4 + 1/4 + 1/4
C’est le processus de division du numérateur en plusieurs unités, qui, ajoutées ensemble, reconstituent la fraction originale.
Exemple 1
Lorsque nous décomposons la fraction 5/6, nous la présentons comme la somme de cinq fractions unitaires 1/6, car la fraction unitaire 1/6 représente une des six parties égales du tout.
Ainsi, 5/8 = 1/8+1/8+1/8+1/8+1/8
Chaque fraction unitaire ⅛ est une partie égale de la fraction originale 5/8. C’est une manière de visualiser et de comprendre comment les fractions composent un tout de manière égale et systématique.
Exemple 2
Pour diviser une fraction en fractions unitaires, nous la transformons en somme de fractions ayant chacune un numérateur de 1. Par exemple, si nous prenons la fraction 4/5, nous pouvons la décomposer en 1/5+1/5+1/5+1/5, puisque chaque 1/5 est une fraction unitaire représentant une des cinq parties égales du tout. Chaque fraction unitaire est une part égale du nombre original et leur somme constitue la fraction d’origine.
Lire aussi : Comment simplifier une fraction au maximum ?
Comment décomposer des fractions en fractions non unitaires ?
Pour décomposer des fractions en fractions non unitaires, nous divisons une fraction en plusieurs fractions plus petites, qui ne sont pas nécessairement des fractions unitaires (avec un numérateur de 1). Cela signifie que nous pouvons utiliser différentes combinaisons de fractions qui, additionnées, correspondent à la fraction originale.
Par exemple, si l’on souhaite décomposer 7/9 , on pourrait la diviser en 3/9 ,1/9, 1/9 et 2/9. Chaque choix représente une façon différente de voir les parties du tout, mais toutes ces parties réunies doivent reformer la fraction de départ.
7/9 = 3/9 +1/9+1/9 + 2/9
Exemple
Prenons un autre exemple : Comment décomposons-nous 12/5
Nous pouvons le décomposer en :
12/5 = 5/5+5/5+2/5
= 1+1+⅖
= 2 + 2/5
Cela nous donne la forme fractionnaire de la fraction
12/5
Comment décomposer des nombres mixtes ?
Pour décomposer des nombres mixtes, on sépare le nombre entier de la fraction propre. Un nombre mixte est donc écrit comme la somme de sa partie entière et de sa partie fractionnaire.
Prenons l’exemple du nombre mixte 1 + 3/4.
Il se trouve entre 1 et 2. Pour le décomposer, on prend le nombre entier, qui est 1, et on l’ajoute à la fraction propre, 3/4. Cela donne 1 + 3/4.
Ce processus nous aide à comprendre et à travailler avec des nombres mixtes en les convertissant en une somme plus facile à manipuler, que ce soit pour des calculs ou pour comprendre des concepts mathématiques.
.
Décomposer une fraction : exercices CM2 / CM1
Voici des exercices sur la décomposition des fractions pour les élèves de cm2 :
- Décompose les fractions suivantes en fractions unitaires :
- 3/4 =
- 5/6 =
- 7/8 =
- Écris chaque nombre mixte comme la somme d’un entier et d’une fraction propre :
- 2 + 1/3
- 5 + 2/5
- 3 + 4/7
- Décompose les fractions suivantes en une somme de fractions avec des numérateurs différents de 1 :
- 6/7 =
- 8/9 =
- 5/8 =
- Trouve deux différentes décompositions pour chaque fraction :
- 4/5 =
- 9/10 =
- 7/12 =
Décomposer une fraction CM1/CM2 : fiches d’exercices à imprimer
Fiche d’exercices 1
Cette fiche offre aux élèves une aventure ludique au cœur des fractions, les invitant à colorier, associer et jouer avec les nombres pour démystifier la décomposition. C’est une exploration visuelle, où chaque fraction se révèle être un puzzle passionnant à construire et à comprendre. Par ces exercices, la magie des mathématiques se dévoile, simple et éclatante.
Télécharger ce fiche de décomposition des fractions CM1/CM2
Fiche d’exercices 2
Cette fiche guide les jeunes esprits à travers les mystères des nombres décimaux avec une simplicité captivante. À travers des lectures, écritures et décompositions méticuleuses, les élèves sont invités à jongler entre les parties entières et décimales, révélant la beauté cachée dans chaque nombre. Parfait pour les CM2, chaque page transforme les défis mathématiques en une clarté limpide.
Télécharger fiche de décomposition des fractions CM2
Fiche d’exercices 3
Cette fiche, destinée aux apprentis mathématiciens en CM2, est un voyage captivant à la découverte des fractions. Chaque exercice est une invitation à décomposer les fractions pour en dévoiler la structure intime, transformant les chiffres et les lignes en un tableau logique. Les élèves y trouvent une clé pour ouvrir les portes de la compréhension numérique, avec une simplicité et une élégance qui rendent l’apprentissage à la fois accessible et fascinant.
Télécharger fiche de décomposition des fractions CM2
Lire aussi : Problèmes fractions CM2 à imprimer
Décomposer une fraction : exercices 6ème
- Décompose les fractions suivantes en une somme de fractions unitaires :
- 4/5
- 6/7
- 9/10
- Donne la décomposition de la fraction 8/12 en utilisant des fractions non unitaires qui ont le même dénominateur.
- Sur une droite graduée, place la fraction 5/4 et décompose-la en une partie entière et une partie fractionnaire.
Décomposer une fraction 6ème : fiches d’exercices à imprimer
Vous trouverez ci dessous des fiches d’exercices sur la décomposition des fractions pour les élèves de 6ème :
Fiche d’exercices 1
Ce document pédagogique, destiné à éclairer les élèves de Sixième, est un parcours structuré à travers le partage et la fraction. Avec des exercices méthodiques allant du calcul mental à la représentation graphique de fractions, il encourage les jeunes esprits à décortiquer les nombres décimaux en leurs composantes fondamentales. Chaque activité est une étape supplémentaire vers la maîtrise des fractions, présentée de manière claire et engageante pour faciliter l’apprentissage et la rétention des concepts mathématiques.
Télécharger cette fiche d’exercices de décomposition des fractions 6ème
Fiche d’exercices 2
Dans ce document pédagogique, les jeunes élèves explorent le monde fascinant des fractions à travers une série d’exercices méthodiques. Ils y découvrent la représentation graphique des fractions, la décomposition en sommes d’entiers et de fractions propres, et même un peu de cryptographie mathématique. C’est un voyage ludique au cœur des nombres, où chaque exercice est une pièce de plus dans le grand puzzle des mathématiques.
Télécharger cette fiche d’exercices de décomposition des fractions 6ème
Fiche d’exercices 3
Ce fichier est un manuel de découverte pour les élèves de 6ème, offrant un périple ludique à travers le territoire des nombres décimaux. Avec des exercices variés, il propose une exploration des écritures décimales, invitant les jeunes mathématiciens à décomposer, recomposer et s’émerveiller devant la précision des chiffres. Des énoncés clairs et des corrigés détaillés accompagnent l’apprenant dans chaque défi, faisant de chaque page une escale enrichissante sur la route de la numération.
Télécharger cette fiche d’exercices de décomposition des fractions 6ème
Fiche d’exercices 4
Le document regorge d’exercices pour affûter la compréhension des fractions chez les élèves de 6ème : des représentations visuelles aux conversions, chaque page est un défi qui allie pratique et théorie, invitant à une exploration approfondie des mystères des nombres.
Télécharger cette fiche d’exercices de décomposition des fractions 6ème
Lire aussi : Exercices fractions 6ème à imprimer

Laisser un commentaire