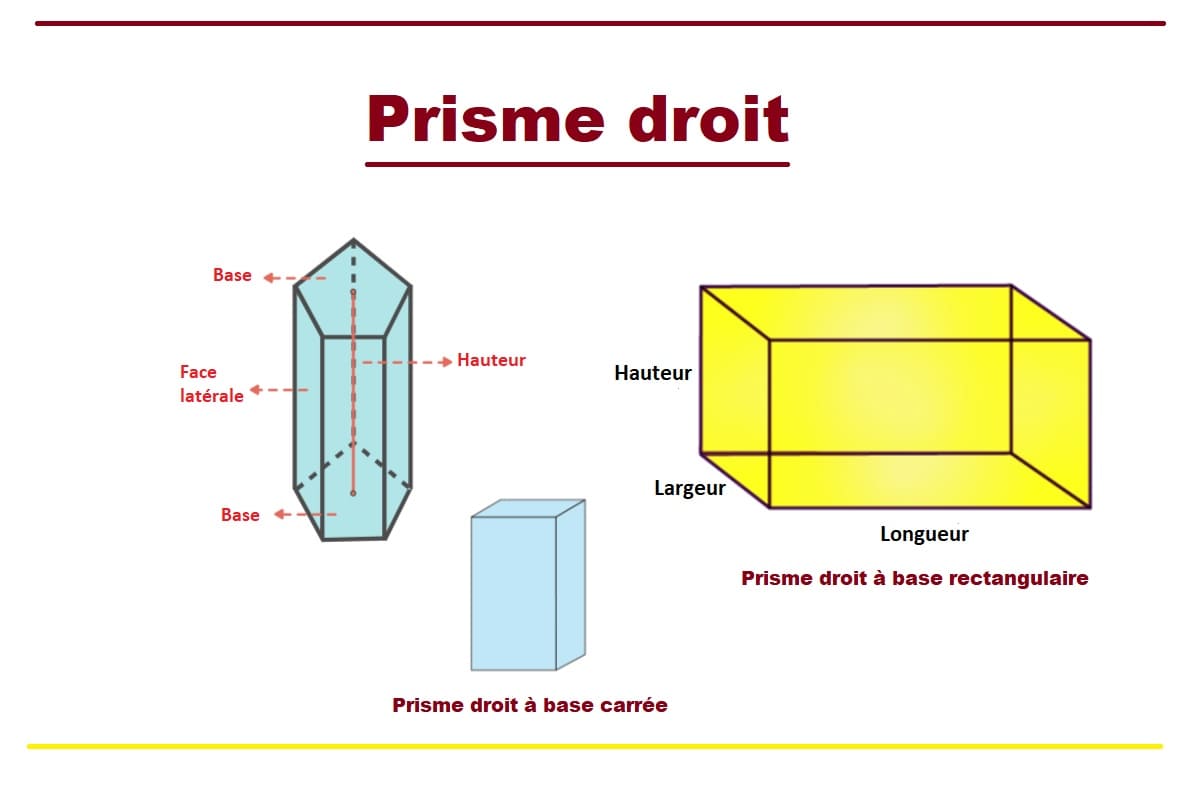
Définition
Un prisme droit est un solide géométrique qui possède :
- Deux bases polygonales identiques et parallèles
- Des faces latérales perpendiculaires aux bases, toutes rectangulaires
Le prisme droit tire son nom de la forme de ses bases. Par exemple, un prisme dont les bases sont des rectangles s’appelle un prisme droit à base rectangulaire.
Vocabulaire essentiel
- Les bases : ce sont les deux faces identiques et parallèles du prisme. Elles peuvent avoir différentes formes : rectangle, carré, triangle, etc.
- Les faces latérales : ce sont les faces qui relient les deux bases. Dans un prisme droit, ces faces sont toujours des rectangles.
- La hauteur : c’est la distance perpendiculaire entre les deux bases. Elle correspond aussi à la longueur des arêtes latérales.
- Les arêtes : ce sont les segments qui forment les contours des faces du prisme.
Utilité en mathématiques
L’étude des prismes droits permet de calculer des volumes d’objets courants : boîtes, aquariums, récipients, emballages. Ces calculs sont utiles dans de nombreuses situations pratiques, notamment pour déterminer la capacité d’un contenant ou optimiser un espace de rangement.
Télécharger Cours Prisme Droit PDF
LES DIFFÉRENTS TYPES DE PRISMES DROITS
On classe les prismes droits selon la forme de leur base. Voici les trois types les plus courants au collège.
Le prisme droit à base rectangulaire (ou pavé droit)
Définition : Un prisme dont les deux bases sont des rectangles identiques.
Particularité : Toutes ses faces (bases et faces latérales) sont des rectangles. C’est pourquoi on l’appelle aussi pavé droit.
Exemples d’objets : boîte à chaussures, aquarium rectangulaire, brique de lait, livre.
Nombre de faces : 6 faces rectangulaires
Nombre d’arêtes : 12 arêtes
Nombre de sommets : 8 sommets
Le prisme droit à base carrée
Définition : Un prisme dont les deux bases sont des carrés identiques.
Particularité : Les bases sont des carrés, et les quatre faces latérales sont des rectangles.
Cas particulier : Si toutes les arêtes du prisme ont la même longueur, le prisme devient un cube.
Exemples d’objets : certaines boîtes d’emballage, colonnes décoratives.
Nombre de faces : 6 faces (2 carrées + 4 rectangulaires)
Nombre d’arêtes : 12 arêtes
Nombre de sommets : 8 sommets
Le prisme droit à base triangulaire
Définition : Un prisme dont les deux bases sont des triangles identiques.
Particularité : Les bases sont des triangles, et les trois faces latérales sont des rectangles.
Exemples d’objets : barre de chocolat Toblerone, toit de maison vu en coupe.
Nombre de faces : 5 faces (2 triangulaires + 3 rectangulaires)
Nombre d’arêtes : 9 arêtes
Nombre de sommets : 6 sommets
Tableau récapitulatif
| Type de prisme | Forme des bases | Nombre de faces latérales | Exemple |
|---|---|---|---|
| Base rectangulaire | Rectangle | 4 | Boîte à chaussures |
| Base carrée | Carré | 4 | Boîte carrée |
| Base triangulaire | Triangle | 3 | Toblerone |
LE VOLUME D’UN PRISME DROIT
Pour calculer le volume d’un prisme droit, on applique la formule suivante :
Volume d’un prisme droit = Aire de la base × Hauteur
Cette formule s’applique à tous les prismes droits, quelle que soit la forme de leur base.
Principe de la formule
Le volume d’un prisme correspond à l’aire de sa base multipliée par sa hauteur. On peut imaginer qu’on empile plusieurs copies de la base jusqu’à atteindre la hauteur du prisme. Le volume total est alors égal à l’aire d’une base multipliée par le nombre de « couches » empilées (la hauteur).
Méthode de calcul
Pour calculer le volume d’un prisme droit, on procède en deux étapes :
Étape 1 : On calcule l’aire de la base en utilisant la formule adaptée à sa forme (rectangle, carré, triangle, etc.).
Étape 2 : On multiplie cette aire par la hauteur du prisme.
Le résultat s’exprime en unités de volume (cm³, m³, etc.).
APPLICATION : CALCULS DE VOLUMES
Cas 1 : Prisme droit à base rectangulaire
Énoncé : Calculer le volume d’un prisme droit dont la base est un rectangle de longueur 4 cm et de largeur 3 cm, et dont la hauteur est de 6 cm.
Résolution :
Étape 1 : Calculer l’aire de la base
La base est un rectangle. On utilise la formule : Aire = Longueur × Largeur
Aire de la base = 4 cm × 3 cm = 12 cm²
Étape 2 : Calculer le volume
On applique la formule : Volume = Aire de la base × Hauteur
Volume = 12 cm² × 6 cm = 72 cm³
Réponse : Le volume du prisme est de 72 cm³.
Pour aller plus loin : Tu peux réviser comment calculer l’aire d’un rectangle, notion utile pour calculer l’aire des bases.
Cas 2 : Prisme droit à base carrée
Énoncé : Calculer le volume d’un prisme droit dont la base est un carré de côté 4 cm et dont la hauteur est de 10 cm.
Résolution :
Étape 1 : Calculer l’aire de la base
La base est un carré. On utilise la formule : Aire = Côté × Côté
Aire de la base = 4 cm × 4 cm = 16 cm²
Étape 2 : Calculer le volume
Volume = Aire de la base × Hauteur
Volume = 16 cm² × 10 cm = 160 cm³
Réponse : Le volume du prisme est de 160 cm³.
Pour aller plus loin : Révise comment calculer l’aire d’un carré pour mieux comprendre le calcul de la base.
Cas 3 : Prisme droit à base triangulaire
Énoncé : Calculer le volume d’un prisme droit dont la base est un triangle rectangle de côtés 3 cm et 4 cm (côtés perpendiculaires), et dont la hauteur est de 5 cm.
Résolution :
Étape 1 : Calculer l’aire de la base
La base est un triangle. On utilise la formule : Aire = (Base × Hauteur du triangle) ÷ 2
Aire de la base = (3 cm × 4 cm) ÷ 2 = 12 cm² ÷ 2 = 6 cm²
Attention : on utilise ici les dimensions du triangle de la base, pas la hauteur du prisme.
Étape 2 : Calculer le volume
Volume = Aire de la base × Hauteur du prisme
Volume = 6 cm² × 5 cm = 30 cm³
Réponse : Le volume du prisme est de 30 cm³.
FORMULES DÉRIVÉES
À partir de la formule générale du volume, on peut déduire d’autres formules utiles pour résoudre différents types de problèmes.
Calculer l’aire de la base
Lorsqu’on connaît le volume d’un prisme et sa hauteur, on peut calculer l’aire de sa base en transformant la formule :
Aire de la base = Volume ÷ Hauteur
Exemple d’application :
Un prisme droit a un volume de 150 cm³ et une hauteur de 10 cm. Calculer l’aire de sa base.
Résolution :
Aire de la base = Volume ÷ Hauteur
Aire de la base = 150 cm³ ÷ 10 cm = 15 cm²
Réponse : L’aire de la base du prisme est de 15 cm².
Calculer la hauteur
Lorsqu’on connaît le volume d’un prisme et l’aire de sa base, on peut calculer sa hauteur en transformant la formule :
Hauteur = Volume ÷ Aire de la base
Exemple d’application :
Un prisme droit a un volume de 200 cm³ et une base dont l’aire est de 20 cm². Calculer la hauteur du prisme.
Résolution :
Hauteur = Volume ÷ Aire de la base
Hauteur = 200 cm³ ÷ 20 cm² = 10 cm
Réponse : La hauteur du prisme est de 10 cm.
Relation entre les trois grandeurs
Les trois grandeurs Volume, Aire de la base et Hauteur sont liées par la formule :
V = A × h
où V représente le volume, A l’aire de la base, et h la hauteur.
Si on connaît deux de ces trois grandeurs, on peut toujours calculer la troisième en réarrangeant la formule :
- V = A × h (pour calculer le volume)
- A = V ÷ h (pour calculer l’aire de la base)
- h = V ÷ A (pour calculer la hauteur)
Télécharger Cours Prisme Droit PDF
Astuce de calcul : Si tu rencontres des difficultés avec les pourcentages ou les conversions dans tes problèmes de géométrie, n’hésite pas à consulter notre guide sur comment calculer un pourcentage.
EXERCICES — LE PRISME DROIT
Ces exercices te permettent d’identifier les prismes droits et leurs caractéristiques.
Exercice 1.
Parmi les affirmations suivantes, indique celles qui sont vraies :
a) Un prisme droit possède deux bases identiques.
b) Les faces latérales d’un prisme droit sont toujours des carrés.
c) Un pavé droit est un prisme droit à base rectangulaire.
d) Un prisme droit à base triangulaire possède 5 faces.
Exercice 2
Associe chaque objet au type de prisme correspondant :
Objets :
- Une boîte à chaussures
- Une barre de Toblerone
- Une boîte d’emballage carrée
Types de prismes :
- A) Prisme à base triangulaire
- B) Prisme à base rectangulaire
- C) Prisme à base carrée
Exercice 3
On te donne un prisme droit à base rectangulaire dont les dimensions sont :
- Longueur de la base : 8 cm
- Largeur de la base : 5 cm
- Hauteur du prisme : 12 cm
Identifie correctement :
- Quelle est la forme de la base ?
- Quelle est la hauteur du prisme ?
- Combien de faces latérales possède ce prisme ?
Exercice 4
Marie observe son aquarium rectangulaire. Elle dit : « Mon aquarium est un prisme droit à base rectangulaire. »
Explique pourquoi Marie a raison en citant les caractéristiques d’un prisme droit que possède l’aquarium.
Exercice 5
Sans calculer, détermine lequel de ces deux prismes droits a le plus grand volume :
Prisme A : Base carrée de côté 5 cm, hauteur 10 cm
Prisme B : Base rectangulaire (6 cm × 4 cm), hauteur 10 cm
Justifie ta réponse en comparant les aires des bases.
Exercice 6
Un prisme droit a pour base un rectangle de longueur 5 cm et de largeur 3 cm. La hauteur du prisme est de 10 cm.
Calcule le volume de ce prisme.
Exercice 7
Un prisme droit a pour base un triangle rectangle dont les côtés perpendiculaires mesurent 3 cm et 4 cm. Le volume du prisme est de 60 cm³.
Calcule la hauteur du prisme.
Exercice 8
Un prisme droit a une base carrée de côté 4 cm et une hauteur de 6 cm.
Calcule l’aire totale de la surface du prisme (aire des deux bases + aire des quatre faces latérales).
Exercice 9
Un aquarium a la forme d’un prisme droit à base rectangulaire. Ses dimensions sont : longueur 50 cm, largeur 30 cm, hauteur 40 cm.
Calcule le volume d’eau que peut contenir cet aquarium lorsqu’il est complètement rempli. Exprime le résultat en cm³, puis convertis-le en litres (rappel : 1 litre = 1000 cm³).
Exercice 10
Un prisme droit a une base carrée de côté 6 cm et une hauteur de 8 cm.
Calcule le volume de ce prisme.
CORRIGÉS
Exercice 1
a) Vrai — Un prisme droit possède toujours deux bases identiques et parallèles.
b) Faux — Les faces latérales d’un prisme droit sont des rectangles, pas nécessairement des carrés.
c) Vrai — Le pavé droit est bien un prisme droit dont les bases sont des rectangles.
d) Vrai — Un prisme à base triangulaire possède 2 bases triangulaires + 3 faces latérales rectangulaires = 5 faces au total.
Exercice 2
- Une boîte à chaussures → B) Prisme à base rectangulaire
- Une barre de Toblerone → A) Prisme à base triangulaire
- Une boîte d’emballage carrée → C) Prisme à base carrée
Explication : On reconnaît le type de prisme en observant la forme de ses bases.
Exercice 3
Forme de la base : Rectangle (longueur 8 cm, largeur 5 cm)
Hauteur du prisme : 12 cm
Nombre de faces latérales : 4 faces rectangulaires
Explication : Un prisme à base rectangulaire possède toujours 4 faces latérales qui relient les deux bases.
Exercice 4
Marie a raison car son aquarium possède les caractéristiques d’un prisme droit :
- Il a deux bases identiques (le fond et le haut de l’aquarium) qui sont des rectangles
- Ces bases sont parallèles
- Les quatre côtés de l’aquarium sont des faces rectangulaires perpendiculaires aux bases
Donc l’aquarium est bien un prisme droit à base rectangulaire.
Exercice 5
Prisme A : Aire de la base = 5 × 5 = 25 cm²
Prisme B : Aire de la base = 6 × 4 = 24 cm²
Le Prisme A a le plus grand volume.
Justification : Les deux prismes ont la même hauteur (10 cm). Le volume dépend donc de l’aire de la base. Comme 25 cm² > 24 cm², le prisme A a un volume plus grand.
Exercice 6
Étape 1 : Calculer l’aire de la base
Aire de la base = Longueur × Largeur = 5 cm × 3 cm = 15 cm²
Étape 2 : Calculer le volume
Volume = Aire de la base × Hauteur = 15 cm² × 10 cm = 150 cm³
Rappel de la formule utilisée : Volume = Aire de la base × Hauteur
Exercice 7
Étape 1 : Calculer l’aire de la base triangulaire
Aire de la base = (3 cm × 4 cm) ÷ 2 = 12 cm² ÷ 2 = 6 cm²
Étape 2 : Calculer la hauteur du prisme
Hauteur = Volume ÷ Aire de la base = 60 cm³ ÷ 6 cm² = 10 cm
Rappel de la formule utilisée : Hauteur = Volume ÷ Aire de la base
Exercice 8
Étape 1 : Calculer l’aire d’une base
Aire d’une base = Côté × Côté = 4 cm × 4 cm = 16 cm²
Étape 2 : Calculer l’aire des deux bases
Aire des deux bases = 2 × 16 cm² = 32 cm²
Étape 3 : Calculer l’aire latérale
Périmètre de la base = 4 × 4 cm = 16 cm
Aire latérale = Périmètre × Hauteur = 16 cm × 6 cm = 96 cm²
Étape 4 : Calculer l’aire totale
Aire totale = Aire des bases + Aire latérale = 32 cm² + 96 cm² = 128 cm²
Méthode : Pour l’aire totale, on additionne l’aire des deux bases et l’aire des faces latérales.
Exercice 9
Étape 1 : Calculer le volume en cm³
Volume = Longueur × Largeur × Hauteur
Volume = 50 cm × 30 cm × 40 cm = 60 000 cm³
Étape 2 : Convertir en litres
Volume = 60 000 cm³ ÷ 1000 = 60 litres
Réponse : L’aquarium peut contenir 60 000 cm³ d’eau, soit 60 litres.
Exercice 3.5
Étape 1 : Calculer l’aire de la base
Aire de la base = 6 cm × 6 cm = 36 cm²
Étape 2 : Calculer le volume
Volume = Aire de la base × Hauteur = 36 cm² × 8 cm = 288 cm³
Rappel : Pour une base carrée, on multiplie le côté par lui-même pour obtenir l’aire.
UN AIDE-MÉMOIRE
Tableau récapitulatif : Types de prismes droits
| Type de prisme | Forme de la base | Formule du volume | Exemple de calcul |
|---|---|---|---|
| Prisme à base rectangulaire | Rectangle (L × l) | L × l × h | 5 × 3 × 4 = 60 cm³ |
| Prisme à base carrée | Carré (c × c) | c² × h | 4² × 5 = 80 cm³ |
| Prisme à base triangulaire | Triangle | (b × h_triangle ÷ 2) × h_prisme | (6 × 4 ÷ 2) × 3 = 36 cm³ |
| Formule générale | Polygone quelconque | Aire de la base × Hauteur | 20 cm² × 10 cm = 200 cm³ |
Formules à retenir
Pour calculer le volume :
V = A × h
où V = volume, A = aire de la base, h = hauteur
Pour calculer l’aire de la base :
A = V ÷ h
Pour calculer la hauteur :
h = V ÷ A
Pour aller plus loin en géométrie
- Comment calculer le volume d’un cône — Découvre d’autres solides
- Comment calculer un périmètre — Révise les bases
- Tableau de conversion en m — Pour convertir les unités de mesure
Caractéristiques communes à tous les prismes droits
- Deux bases identiques et parallèles
- Faces latérales rectangulaires
- Hauteur perpendiculaire aux bases
- Volume = Aire de la base × Hauteur